Loop-Quantengravitation (Versuch einer laienhaften Veranschaulichung)

Der vorhergehende Beitrag “Zurück vor den Urknall” – ein Buch v. Martin Bojowald" befasst sich mit der Ausgangslage zur Entwicklung der Quantengravitation sowie möglichen Konsequenzen, die sich aus einer ihrer Varianten, der LQG ergeben könnten.Die nachfolgenden Erläuterungen gehen teilweise doch sehr ins Detail, obwohl sie die Thematik nur an der Oberfläche streifen. Dabei sind die Einschübe in kleiner Schrift als Ergänzung aufzufassen..

Physikalische Theorien dienen dazu, den Aufbau der Natur und die verschiedenen in ihr wirksamen Kräfte (oder 'Wechselwirkungen') zu beschreiben. Das Ziel einer Vereinheitlichten Theorie, insbesondere der Quantengravitation wird nachvollziehbar anhand eines Überblicks darüber, was die Physik bisher in dieser Richtung veranstaltet haben - und was sie dabei heraus fanden. Einen überschaubaren und vor allem verständlichen Rückblick legt G. Münster mit der Abhandlung "Atome, Quarks, Superstrings - Auf der Suche nach der Weltformel" vor.
In wenigen Worten soll die Quantengravitation die beiden großen physikalischen Theorien des 20. Jahrhunderts - die Quantentheorie und die Allgemeine Relativitätstheorie (als ART abgekürzt) - vereinigen.

Quantengravitation als Brücke

Allgemein hat sich die Quantentheorie als der Rahmen zur Beschreibung von drei Wechselwirkungen etabliert; mit der Quantenfeldtheorie (QFT) lassen sich Wahrscheinlichkeiten bestimmter Teilchenprozesse ebenso berechnen wie die Existenz zuvor unbekannter Elementarteilchen. Sie erklärt auch, wie aus mikroskopischen Partikeln neue Teilchen entstehen können. Dagegen konnte die Gravitation als vierte Kraft bisher nur durch die ART erklärt werden. Doch die Physik möchte alle Naturkräfte in einem einzigen umfassenden und schlüssigen System beschreiben.

Wie bereits dargelegt, ergeben Berechnungen zum Urknall mit Hilfe der ART unendliche Wahrscheinlichkeiten oder eine Null im Nenner (vgl. Singularitäten-Theoreme v. R. Penrose und St.Hawking) ...beides ist bei Naturwissenschaftlern unbeliebt).
Doch ohne die ART kann die gesamte Natur auch nicht erklärt werden, denn sie beschreibt neben der Schwerkraft auch die Geometrie der Raumzeit.

Gesucht wird: eine noch fundamentalere Theorie, welche solche Singularitäten vermeidet und die Physik selbst unter so extremen Bedingungen beschreiben kann. In Entwürfen einer Theorie der Quanten-Gravitation bedeutet nicht bilden die Prinzipien von ART und QFT wichtige Teile eines übergeordneten Konzepts.

Ein derartiger Ansatz mit der Bezeichnung Schleifen- oder Loop-Quantengravitation (nachfolgend mit LQG abgekürzt) zielt darauf ab, "die Prinzipien der ART und der QFT konsistent zu verknüpfen und dabei eine hintergrundunabhängige Quantisierung der Gravitation zu ermöglichen".
Stark verkürzt besagt die LQG, dass Raum und Zeit analog zum Aufbau der Materie aus nicht weiter teilbaren Einheiten bestehen. Diese "Raum-Zeit-Atome" sind kleinste ringförmige Gebilde, auch Loops oder Schleifen genannt. Die Ausdehnung der Loops liegt im Bereich von '10 hoch minus 32' Millimetern, der Planck-Länge.

Quantisierung der Raumzeit?

Um eine ungefähre Idee vom Vorgehensmodell der LQG zu erhalten, richtet sich der Blick zunächst auf einen Vorgang namens Quantisierung (platt formuliert: die Zerstückelung in winzige, aber voneinander klar unterscheidbare Teilchen bzw. Einheiten). In der Physik kennzeichnet sie den Übergang von einer klassischen Theorie zu einer Quantentheorie, denn sie berücksichtigt drei Konsequenzen, die sich aus der Quantenphysik ergeben haben:

• Es lassen sich nur noch Wahrscheinlichkeiten angeben, mit denen der Impuls oder die Position des Teilchens einen bestimmten Wert annehmen.
• Als Folge der Heisenbergschen Unschärferelation können Position und Impuls nicht mehr gleichzeitig beliebig genau bestimmt werden.
• Größen, die in der klassischen Theorie beliebige Werte annehmen können, nehmen in der Quantentheorie nur noch bestimmte, diskrete Werte an. Sie treten also in quantisierter Form auf.

War man bis ins vorletzte Jahrhundert noch überzeugt, dass Materie sich bis ins Kleinste als Kontinuum verhält, wies die Entwicklung der Quantenmechanik zu Beginn des 20. Jahrhunderts nach, dass die Materie aus 'zählbaren Stücken' besteht (so gibt es tatsächlich Annahmen über die Anzahl aller kleinsten Teilchen im Universum - eine Zahl mit weit mehr als hundert Nullen).

Auf der Suche nach einer Theorie der Quantengravitation wurde nun die Frage aufgeworfen, ob der Raum kontinuierlich sei oder aus diskreten Einheiten bestehe: Waren 'Atome des Raumes' entgegen jeder Alltagswahrnehmung vorstellbar – Volumenelemente, die sich nicht noch weiter aufspalten lassen? Die gleiche Frage wandte man analog auf die Zeit an: Entwickelt sich die Natur kontinuierlich oder in winzigen Schritten?

Die Körnigkeit von Raum und Zeit (Raumzeit) steht in einem engen Zusammenhang mit der angestrebten Quantentheorie der Gravitation.

['Diskret' hat hier nichts mit Verschwiegenheit zu tun (war klar, oder?), sondern bezeichnet in der Mathematik und Physik endliche oder zumindest abzählbar unendliche Mengen. Um etwas zählen zu können, muss eine Unterscheidbarkeit der einzelnen Teile bzw. Einheiten gegeben sein.
Der Ausdruck 'Loop' (=Schleife) komme übrigens daher, dass in dieser Theorie gelegentlich mit winzigen Schleifen in der Raumzeit operiert werde.]

Mitte der 1980er Jahre wiederholten Abhay Ashtekar, Ted Jacobson Carlos Rovelli den bis dahin stets gescheiterten Versuch, die Quantenmechanik mathematisch widerspruchsfrei mit der ART zu kombinieren. Ihnen war bewusst, dass die bislang negative Resultate aus den früheren Jahren eine wichtiges Lücke offen ließen: damalige Berechnungen hatten stets unterstellt, die Geometrie des Raumes sei selbst bei beliebig starker Vergrößerung kontinuierlich und glatt – so wie man es früher auch von der Materie angenommen hatte. Diese Unterstellung des kontinuierlichen Raumes war bislang als zwingend notwendig erachtet worden. Jetzt suchten Ashtekar und seine Kollegen nach einem Berechnungsverfahren, das keinen glatten und kontinuierlichen Raum voraussetzte. (Bei näherem Interesse → Ashtekar-Variablen; für ein erstes Grundverständnis bedarf es dieser Informationstiefe m.E. aber nicht).

Die Vielzahl der Möglichkeiten eines Übergangs wurde durch zusätzliche sinnvolle Annahmen begrenzt; eine bestimmte Form der Quantisierung wurde selektiert. Alle Annahmen folgten den die experimentell erprobten Prinzipien von ART und Quantentheorie - insbesondere auf zwei Grundprinzipien der ART wurde Wert gelegt:
Hintergrund-Unabhängigkeit - besagt, dass die Geometrie der Raumzeit feststeht, sondern eine sich entwickelnde dynamische Größe ist.
Diffeomorphismus-Invarianz - besagt, dass man ein beliebiges Koordinatensystem wählen darf, um die Raumzeit darzustellen. Ein Punkt in der Raumzeit ist nur durch die physikalischen Vorgänge in diesem Punkt definiert, nicht durch seinen Ort in einem speziellen Koordinatensystem (→ Anmerkungen ganz unten)

Mathematische Berechnung ergaben tatsächlich gequantelten Raum. Wie neuere Forschungsarbeiten zeigten, gibt gerade die zusätzliche Annahme der Hintergrundunabhängigkeit eine Quantisierung eindeutig vor (→ LOST-Theorem).



Damit war der Grundstein zur Theorie der Loop-Quantengravitation gelegt - die Quantisierung ersetzt in der LQG die kontinuierliche Vorstellung von Raum und Zeit durch eine eine diskrete Raumzeit-Struktur. Nach und nach Laufe entwickelte sich die LQG unter weltweiter Beteiligung zu einem eigenen Forschungsgebiet - und ein völlig neues Bild der Raumzeit (vgl. Erläuterung) zeichnete sich ab:

Betrachtet wurde, was die Theorie über ein kleines Volumen (oder eine Fläche) aussagt. Weil die Quantenphysik eine präzise Festlegung der zu messenden physikalischen Größen erfordert, wurde eine Hülle H definiert (z.B. Materie, etwa eine metallene Hohlkugel die Geometrie der Raumzeit selbst definiert – der Ereignishorizont eines Schwarzen Lochs).
Wird nun das Volumen dieser Hülle gemessen, lassen Quantentheorie und Diffeomorphismus-Invarianz zwei Arten von Resultaten zu:

• Wenn die Geometrie des Raumes kontinuierlich ist, könnte das Volumen beliebig klein sein, und das Messergebnis wäre eine positive reelle Zahl, die beliebig nahe bei Null liegen könnte.
• Doch bei körniger Geometrie kann die Messung nur diskrete Zahlenwerte ergeben, die nie kleiner werden können als ein bestimmtes minimales Volumen.

Untersucht man, wie viel Energie die um einen Atomkern kreisenden Elektronen besitzen, ist der klassischen Mechanik zufolge ist jeder Energiebetrag möglich. Doch die Quantenmechanik erlaubt nur bestimmte Energiewerte und verbietet alle, die dazwischen liegen. Analog verhält sich der Raum: Eine Volumenmessung kann nur diskrete Zahlenwerte ergeben, auch die Fläche der Hülle H ist diskret. Der Raum ist also nicht kontinuierlich, sondern existiert in Form von Quanten für Fläche und Volumen.

Spin-Netzwerke als mathematisches Grundgerüst der LQG

Quantenzustände von räumlich eingeschränkten Volumina und Flächen lassen sich mit Hilfe eines bestimmten Formalismus grafisch darstellen: Räume werden darin durch so genannte Spin-Netzwerke abgebildet, indem der kontinuierliche Raum durch ein feines Netzwerk von eindimensionalen Kanten ersetzt wird. (Die Bezeichnung dieser Spin-Netzwerke kommt zustande, weil die enthaltenen Zahlen mit einer physikalische Größe namens Spin verwandt sind).

Die LQG beschreibt den Raum also nicht als kontinuierliches Gebilde, sondern durch ein solches Spin-Netzwerk verschiedener Kanten, die in Knotenpunkten, so genannten Vertizes, aufeinander treffen. Auf großen Skalen, bei denen Quantengravitationseffekte vernachlässigbar sind (also quasi aus der Ferne betrachtet), erscheint dieses feine Netz weiterhin als Kontinuum. Wenn man jedoch zu Längenskalen nahe der so genannten Planck-Skala (s.u.) zoomt, dann zeigt sich der zunächst kontinuierlich erscheinende Raum in Wirklichkeit als ein aus feinsten Gebilden aufgebautes Netzwerk.

[Die nach Max Planck benannte Planck-Skala markiert eine Grenze für die Anwendbarkeit des Standardmodells der Teilchenphysik und der ART. Unterhalb einer kleinsten Distanz, der sog. Planck-Länge, versagen alle Modelle. Zur Veranschaulichung: Die Planck-Länge lP ist um einen Faktor von etwa 1020 kleiner als der Durchmesser eines Protons und damit jenseits einer direkten experimentellen Zugänglichkeit.]

Name	Größe	Dimension	Term	Ungefähres SI-Äquivalent	Andere Äquivalente
Planck-Masse	Masse	M		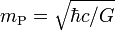2,17651 · 10−8 kg	1,311 · 1019 u
Planck-Länge	Länge	L		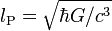1,616199 · 10−35 m	3,054 · 10−25 a0
Planck-Zeit	Zeit	T		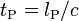5,39106 · 10−44 s
Planck-Ladung	Ladung	Q		1,8755459 · 10−18 C	11,70624 e
Planck-Temperatur	Temperatur	Θ		1,416833 · 1032 K

Übersicht der Planck-Einheiten (Quelle: Wikipedia)

Weil die LQG keine beliebig kleinen Flächen- und Volumeninhalte mehr erlaubt, sondern nur noch Vielfache von deren Quanten (bestimmte diskrete Werte - kleinste Flächeninhalte, die nicht unterschritten werden dürfen), werden die verwendbaren Werte für Volumen und Fläche durch Einheiten der o.a. Planck-Länge vorgegeben. Sie gibt mit nur 10^–33 Zentimetern die Größenordnung an, ab der die Geometrie des Raumes nicht mehr kontinuierlich ist. Die kleinstmögliche Fläche (=Flächenquant) liegt bei etwa 10^-33 Quadratzentimeter, und das kleinste Volumen (=Volumenquant) beträgt rund 10^-99 Kubikzentimeter. Umgerechnet existieren in jedem Kubikzentimeter des Raumes rund 10⁹⁹ Volumenatome.

Aus diesen Rahmenvorgaben ergeben sich Regeln für die grafische Darstellung der Raumgeometrie: Ein Flächenquant wird als eine Linie dargestellt; eine aus vielen Quanten zusammengesetzte Fläche entspricht somit einer Vielzahl von Linien. Ebenso steht ein Knoten für ein Volumenquant, während ein größeres Volumen viele Knoten beansprucht.

Die einzelnen Knoten und Linien repräsentieren denkbar winzige Raumgebiete: Ein Knoten entspricht einem Planck-Volumen (Kubik-Planck-Länge) und eine Linie einer Planck-Fläche (Planck-Länge zum Quadrat). Doch mit Vielfachen dieser Einheiten lässt sich jede Hülle 'ausmessen' - der Größe und Komplexität solcher Spin-Netzwerke sind nach oben keine Grenzen gesetzt - um den Quantenzustand des gesamten Universums abzubilden, würde man ein gigantische Spin-Netz mit etwa 10¹⁸⁴ Knoten benötigen.

Ich stelle mir dies so vor, als sollte ich eine Wand mit einem Bild versehen. Statt Pinsel und Farbe zum Ausmalen glatter (kontinuierlicher) Flächen und Linien stehen mir normierte, sehr kleine Mosaiksteine ('diskrete Einheiten') zur Verfügung, mit denen ich freilich das gleiche visuelle Resultat erzielen kann wie mit einem Pinsel (ist nur sehr viel mehr Arbeit). Stehe ich unmittelbar vor meinem fertigen Bild bzw. Mosaik, wird dessen feine Struktur sichtbar; trete ich aber etliche Schritte zurück, so verschwimmen die Steinchen bald zu einem scheinbar glatten Bild ohne erkennbare Einzelteile. Mit den Pixeln am PC-Bildschirm verhält es sich wohl ähnlich.

Denn das Wichtigste fehlt bislang noch - der 'Inhalt' der beschriebenen Räume: Materieteilchen und Energieeinheiten werden als bestimmte Typen von Knoten mit einer zusätzlichen Beschriftung dargestellt. Elektromagnetische und andere Felder werden durch zusätzliche Angaben auf den Linien dargestellt. Soll Bewegung von Teilchen und Feldern durch den Raum visualisiert werden, geschieht dies, indem man diese Beschriftungen in diskreten Schritten auf den Graphen verschiebt.

Um zuletzt auch die Zeit als eine weitere Dimension abzubilden, werden die Spin-Netzwerke (die in der LQG den Raum darstellen) zu Spin-Schäumen erweitert und damit dem Begriff der Raumzeit (der Vereinigung von Raum und Zeit in der ART) angepasst. Durch Hinzufügen der Zeit verwandeln sich die Linien der Spin-Netzwerke in zweidimensionale Flächen, aus den Knoten werden Linien. (Zwei Begriffe sind hierbei nicht zu verwechseln: Während der Quantenschaum die gekrümmte, schaumartige Raumzeit des Quantenvakuums zu einem gegebenen Zeitpunkt bezeichnet, ist der Spin-Schaum nicht 'real', sondern eine formale Darstellungsweise):

Spin-Schaum durch zeitlich (t) diskretes
Fortschreiben eines Netzwerkes

Auch die Zeit nimmt in der LQG einen diskreten Charakter an; sie wird hier definiert durch die Abfolge diskreter Züge, die das Netzwerk (den Raum) umordnen. Zeit fließt nicht kontinuierlich, sondern ist nun diskret und 'hüpft' in kleinen Intervallen - vergleichbar den in Zeitlupe sichtbaren Einzelbildern eines (Zelluloid-)Films. Sie tickt gewissermaßen wie eine Uhr, wobei jedes Ticken ungefähr einer Planck-Zeit (10–43 Sekunden) entspricht.

Damit ist das Handwerkzeug erst mal komplett: Durch die Formalisierung und Quantisierung von Raum und Zeit in Spin-Netzwerken und -Schäumen erhielt man eine Theorie zur Vorhersage präziser Quantenwahrscheinlichkeiten - ein klar definiertes Verfahren zur Berechnung der Wahrscheinlichkeit jedes Vorgangs in einer Welt, die den Regeln dieser Theorie gehorcht.

Loop-Quantenkosmologie - Bezug zur ART und 'unserer' Realität?

Das 'Endziel' ist also noch nicht erreicht, denn bis hierhin ermöglicht die LQG macht Aussagen über Raum und Zeit lediglich in den Größenordnungen der unfassbar winzigen Planck-Skala. Eine Überprüfung der Theorie wird zeigen müssen, ob die makroskopisch angelegte ART als klassische Näherung der LQG hergeleitet werden kann - indem Spin-Netzwerke sie über sehr viele Planck-Längen gemittelt werden.

Zunächst erscheint jede experimentelle Überprüfung der LQG schlicht unmöglich, weil ihre charakteristischen Effekte erst im Planck-Maßstab von Bedeutung sind. Mit irdischen Teilchenbeschleunigern kann der Planck-Maßstab jedenfalls nicht erreicht werden.

Doch könnte die Ausbreitung des Lichts im Universum eine Hilfestellung geben, denn bestimmte Effekte - wie die Brechung von Licht und seine Aufspaltung verschiedener Wellenlängen zu einem farbigen Spektrum - treten auch auf, wenn Licht und Teilchen den diskreten Raum eines Spin-Netzwerks durchqueren.

Zwar sind für jede nachweisbare Strahlung die Effekte der körnigen Raumstruktur zwar äußerst gering - doch sie akkumulieren sich, wenn das Licht große Entfernungen zurücklegt. Deshalb beobachtet man Licht und Teilchen, die Milliarden von Lichtjahren unterwegs waren, etwa von Gammastrahlen-Ausbrüchen.-

Die makroskopisch relevante ART erlaubt die Voraussetzung des kosmologischen Prinzips, welches zwei Grundannahmen von Modellen über 'das Universum als Ganzes' zusammenfasst:

• Das Weltall ist homogen – das heißt, es stellt sich einem Beobachter unabhängig von dem Punkt des Raumes, in dem er sich befindet, immer gleich dar (Prinzip der Homogenität, auch kopernikanisches Prinzip genannt). 
• Das Weltall ist isotrop – das heißt, es stellt sich dem Beobachter unabhängig von der Beobachtungsrichtung im Raum immer gleich dar (Prinzip der Isotropie).
• Die damit verknüpfte, als homogen (unabhängig vom Ort) und isotrop (unabhängig von der Richtung) bezeichnete Symmetrie schränkt die mögliche Form der Raumzeit-Geometrie schon erheblich ein. Durch diese "Symmetriereduktion" lassen sich sich die Gleichungen der ART so weit vereinfachen, dass sie explizit lösbar sind.

In der LQG, die ja eine 'Theorie von Allem' werden soll, stellt sich die Voraussetzbarkeit dieser Symmetriereduktion komplizierter dar - an ihr wird zur Zeit noch gearbeitet. Derweil hat sich ein symmetriereduzierter, kosmologischer Sektor der LQG herausgebildet (eine Abkürzung?), der auch als Loop-Quantenkosmologie (LQC) bezeichnet wird.

Der bereits erwähnte Physiker Martin Bojowald hat Teile der LQC entwickelt, um typische Eigenschaften der LQG in einfachen Modellen zu erforschen. Hierbei werden die vereinfachten Einstein-Gleichungen quantisiert, was auf ebenfalls einfachere "Quanten-Einstein-Gleichungen" führt, die sich wiederum explizit lösen lassen.

Ausblick

Bemerkenswert an der LQC ist, dass die in der ART auftretende Urknallsingularität nicht mehr vorhanden ist: Folgt man im Rahmen der LQC der Entwicklung des Universums rückwärts in der Zeit, so führt dies nicht zum Urknall, sondern durch Quanteneffekte entsteht eine zusätzliche abstoßende Kraft, die das Universum, bevor es in eine Singularität läuft, abprallen und wieder expandieren lässt.

• Ungeklärt ist allerdings bislang, ob sich die Singularitäten auch in der kompletten LQG auflösen lassen - daran wird derzeit im Rahmen so genannter "Spin-Schaum-Modelle" wird intensiv geforscht.
• Ebenso untersuchen die LQG-Theoretiker, in welchem Maße die LQG konsistent mit den bereits bestehenden und z.T. experimentell überprüften Theorien ist.

Solchen Konsistenzprüfungen unterliegt jeder Versuch einer Quantengravitationstheorie stellen. Deshalb spricht Martin Bojowald vom hochspekulativen Charakter seiner Interpretation der LQG. Erst wenn die neue Variante diese Tests besteht, lohnt es sich ernsthaft darüber nachzudenken, wie sie unser bisheriges Verständnis der Physik und des Universums verändert...

Anmerkungen

Zu dem etwas sperrigen Begriff "Diffeomorphismus-Invarianz":

In seinem Astro-Lexikon auf Astrowissen.de beschreibt Andreas Müller die Hintergrundunabhängigkeit als anschauliche Übersetzung einer von der ART diktierten Eigenschaft namens Diffeomorphismusinvarianz: Ein 'Hintergrund' sei eine nicht-dynamische (also statische Struktur), auf der die physikalischen Objekte agieren ("die Bühne der Physik").

Die ART sagt nun, dass es diese statische Bühne nicht gibt! "Es ist nicht von Belang, wo die physikalischen Objekte in einer Raumzeit lokalisiert sind (absolute Positionierung), sondern wie sie relativ zueinander stehen (relationale Positionierung). Der Diffeomorphismus bewerkstelligt gerade mathematisch eine 'Verschiebung' der dynamischen, physikalischen Objekte..."

Alternativen zur LQG

Das Verständnis der Merkmale und Besonderheiten der Schleifen- oder Loop-Quantengravitation erschließt auch aus ihrer Gegenüberstellung mit zwei weiteren Kandidaten für eine Vereinheitlichte Theorie aller vier Grundkräfte:

• Bei der String- bzw. Superstringtheorie handelt es sich die konservativere Variante, die von kleinsten Materieeinheiten (den Strings) - ausgeht, die in einer extern fließenden Zeit existieren, so dass die Frage nach deren Wesen ausgeklammert bleibt.Stephen Hawking spricht von einer "Harmonie stiftenden Möglichkeit", falls die String- und LQG-Theoretiker im Grunde dieselbe Theorie entwickeln, nur von vollkommen verschiedenen Ausgangspunkten aus: "Beide Theorien gehen von Schleifen aus - die Stringtheorie von Stringschleifen, die Schleifen-Quantengravitation von 'elementaren Raumschleifen -, daher liegt der Schluss einer möglichen Verbindung nahe. Dafür spricht auch der Umstand, dass die beiden Theorien bei den wenigen Problemen, die ihnen beiden zugänglich sind - etwa der Entropie Schwarzer Löcher -, vollständig übereinstimmen..."
• Einen dritten Weg zur Quantengravitation könnte die Kombination der Prinzipien von ART und QFT eröffnen - die von dem theoretischen Physiker Prof. Claus Kiefer favorisierte "Quantenkosmologie". Kiefer setzt nicht bei der Mikrophysik an, sondern beim Kosmos insgesamt, er arbeitet nicht mit kleinsten Objekten wie Strings oder Loops, sondern mit einer „kanonischen Quantisierung“. Dies ist der Name eines bekannten Verfahren der Quantentheorie, welches die Basisgrößen Ort und Impuls durch zwei geometrische Eigenschaften des Raumes ersetzt. Auf diesem Wege soll das Universum durch eine einzige mathematische Funktion beschrieben werden, die einer einzigen Grundgleichung genügt und in der keine Zeitvariable mehr vorkommt. 

Siehe auch:
Artikel "Quanten der Raumzeit" v. Lee Smolin, erschienen im Spektrum der Wissenschaft im März 2004.

---

Max Planck und die Quantenphysik